Cleaning non positive semidefinite correlation matrices
Estimation of a valid instantaneuos or forecasted correlation matrix is an important problem in the field of derivatives valuation and of risk management. In one among many plausible situations, a risk manager might want to study the impact of bumping or overriding the equity correlation matrix. He might not end up generating spurious results e.g. negative VaR numbers if he does not use a consistent correlation matrix. A valid correlation matrix not only has to be symmetric but also positive semidefinite. In another situation, a trader or a quant might have problems in valuing monte carlo based multi asset trades because Cholesky decomposition of a correlation matrix requires the matrix to be positive semidefinite.
The Positive Semidefinite requirement
A correlation matrix must be positive semidefinite. This can be tested easily. If all the eigenvalues of the correlation matrix are non negative, then the matrix is said to be positive definite.
Let's take a hypothetical case where we have three underliers A,B and C. The returns of underliers A and B are perfectly correlated i.e. ρAB=1 and the returns of the underliers B and C are also perfectly correlated i.e. ρBC=1. Now if the returns of the underliers A & B are directly proportional and at the same time if the returns of the underliers B & C are also directly proportional, we know that the returns of the underliers A & C cannot be inversely related e.g. ρAC cannot be -1 .

To find the eigenvalues of this matrix we need to calculate the solutions to the characteristic equation, Det(A-λI)=0, where I is the identity matrix and the roots λ of the characteristic equation are said to be the eigenvalues of the correlation matrix A.

We get the eigen values of A = {2,2,-1}.
We conclude that A is not positive semidefinite and hence an invalid correlation matrix as one of the eigen values is negative(λ = -1).
Cleaning the spurious correlation matrix
There are many methods used in practise but we are going to discuss the Spectral decomposition (also known as principal component analysis) of treating the correlation matrix. The method is described in steps below:
1. Take the correlation matrix  (which is not positive semidefinite i.e. atleast one eigenvalue is negative) and calculate the eigen value diagonal
(which is not positive semidefinite i.e. atleast one eigenvalue is negative) and calculate the eigen value diagonal  matrix and matrix
matrix and matrix  comprising of eigenvectors
comprising of eigenvectors  in the ith column of the Matrix.
in the ith column of the Matrix.
We have,  [EV Decomposition]
[EV Decomposition]
2. Set negative elements of the diagonal matrix  to 0 i.e. set all negative eigenvalues
to 0 i.e. set all negative eigenvalues 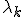 of the correlation matrix
of the correlation matrix  to Zero. Let the new matrix represented as
to Zero. Let the new matrix represented as  made up with new set of eigenvalues
made up with new set of eigenvalues 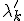
3. Calculate the diagonal scaling matrix 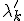 whose elements are defined by
whose elements are defined by
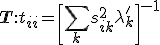
4. Calculate new matrix 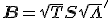
5. The new correlation matrix 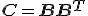
Example
Let the correlation matrix from the example above 
We have,

such that,

Setting negative eigenvalues to 0 we have,
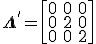
Calculate diagonal scaling matrix
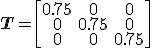
It follows that,
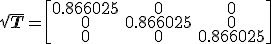
[remember that square root of a diagonal matrix is simply a diagonal matrix whose elements are square root of elements from the original matrix]
Similarily,
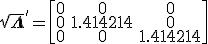
Calculating 
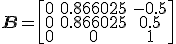
Our new correlation matrix 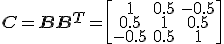
Download excel spreadsheet example
The example has a dependancy on on Matrix functions library which is attached within the zip file. Other quantobjects libraries and their documentation are available here - Quant Libraries.
For comments and feedback, feel free to write to us at feedback@deltaquants.com
References
1. Rebonato, Riccardo and Jackel, Peter [19th October 1999]- "The most general methodology to creat a valid correlation matrix for risk management and option pricing purposes"









